生物数学（mathematical biology 或biomathematics）是数学与生命科学、生物学、农学、医学和公共卫生等学科互相渗透、融合而形成的交叉学科。它运用数学方法和技巧研究并解决上述应用领域的具体实际问题，并对相关的数学方法进行深入理论研究，兼有生命科学思想和量化科学思想的特征。

　　生物数学为各学科领域提供了强大的理论保证与快捷的计算工具，有助于人们更早地发现和掌握自然界的生态规律。其核心方法为：将所关心的生物学对象数量化，并用数量关系来描述这些生物学过程。数量化的实质就是建立数学模型，并定量地描述生命运动的过程。通过数量化，一个复杂的生物学问题就能转变成一个数学或统计问题，通过对数学或统计模型的理论分析、求解和数值模拟，就能够获得对生物现象的深刻认识，从而揭示生命现象的变化规律，达到对生命科学问题解释、预测的目的。例如，经典Volterra 模型揭示的Volterra 原理，能够帮助生物学家解释生物资源管理与有害生物控制中很多棘手的问题。

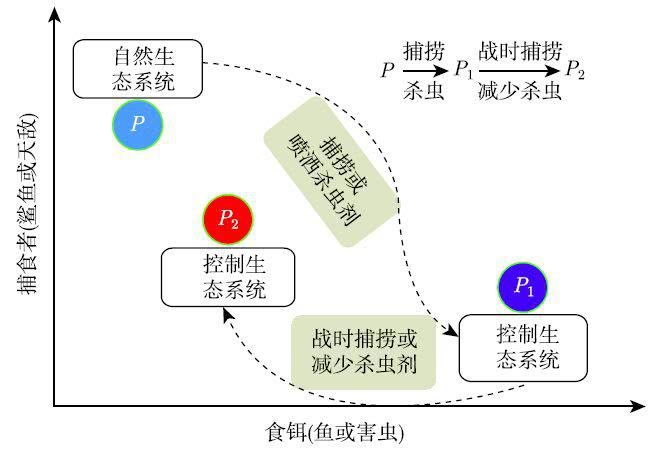　　▲ Volterra 原理在渔业资源和害虫控制中的应用说明

　　生物数学已有百年的历史。

　　20 世纪初期数学在种群生态学、传染病动力学和数量遗传学中的广泛应用是生物数学发展史上的第一次辉煌。对上述三个领域系统研究过程中提出的模型思想和研究方法（比如竞争排斥原理、Volterra 原理、Hardy-Weinberg 平衡原理和传染病模型中的阈值理论）已经被生物学家广泛接受，有些原理已经广泛地应用到生物数学的其他分支。

　　到20 世纪中叶生物学与其他学科的交叉，特别是数学和计算机技术的进一步发展，在人体和细胞等复杂系统研究方面取得的突破性进展，使生物数学的研究获得了一次新的飞跃。

　　随着生物数学新的分支：生物信息学和系统生物学的产生，特别是数据科学与人工智能在生物数学领域的广泛应用，生物数学必将成为世界科学研究最为引人注目的交叉研究领域之一。

　　《生物数学》（唐三一等编著. 北京：科学出版社，2020. 4）以编者多年来从事生物数学的教学和研究工作为背景，介绍生物数学的基本概念、研究方法和最新成果，比如，数学模型建立的原理、生物学数据处理的方法和数学模型分析的技巧等，希望能将对生物数学有兴趣的读者从初学引导到科研前沿。

　　本书编写力求基础，突出应用性，做到内容丰富、论述详细、方法实用、尽量满足不同专业本科生和硕士研究生学习的需要，力图使只要学过高等数学的学生就能完成本书大部分内容的学习。

　　由于生物数学涉及的领域众多，一部基础教材不可能包罗万象。因此本书的内容将集中于数学模型在种群生态学、传染病动力学、药物动力学、病毒动力学、酶动力学、细胞和分子生物学、生物统计学等领域中的典型实例应用方面。

　　每一部分的引入和构建都秉承以实际问题为驱动、以解决实际问题为导向，重点回答：

　　根据实际问题或数据如何建立、发展适当的数学模型？

　　是否存在建立此类模型的一般性原理？

　　改进模型的基本原理是什么？

　　如果对这些问题有了基本的了解，这将有助于读者了解数学在生物学中应用的一些基本思想，理解模型发展的思路：模型建立—模型求解—模型细化，掌握处理一些应用问题的方法以及领会理论和方法在解决实际问题中的重要价值。本书旨在为读者迅速了解生物数学的本质提供素材，为致力于生物数学研究的读者提供一个掌握研究方法的平台。

　　生物数学的本质是生物学与数学的交叉和融合，其研究是以问题驱动或数据驱动为基础的。现如今是大数据和人工智能时代，如何基于数据，发展相应的统计分析、计算方法对实验、观测等数据进行分析，特别是通过参数估计与模型辨识如何实现模型与数据的对接，是生物数学入门阶段必须掌握的技巧和方法。如何有效地利用具有随机因素的观察统计和实验数据来确定模型参数，即模型识别的问题，需要借助生物统计学、数据处理、参数估计和数值实现等综合的方法进行研究。关于数据处理和模型参数估计方法用专门章节介绍，而数值研究方法则贯穿全书，书中涉及的数学软件有MATLAB，Maple 和Xppaut，我们将根据具体研究问题介绍有关数学软件在生物数学中的应用。

　　书中主要章节的内容相对独立，有利于不同专业的读者根据需要进行取舍。再者，在很多章的最后一或两节增加了国内外有关研究资料和作者所在研究组近几年的研究成果，力求由浅入深，通俗易懂，以便读者能够在生物数学入门的学习阶段就能了解有关最新动态。