2020年诺贝尔物理学奖被授予罗杰·彭罗斯(Roger Penrose)，莱因哈特·根策尔(Reinhard Genzel)，和安德里亚·格兹(Andrea Ghez)，奖励他们三人在黑洞研究方面作出的杰出贡献。

三位获奖者中年纪最大的罗杰·彭罗斯爵士出生于1931年，是一位英国数学家、物理学家和科普作家。他的原始获奖工作是一篇只有三页的数学论文，用广义相对论推导出了黑洞的存在。这是诺贝尔物理学奖第一次颁发给一个纯数学工作。彭罗斯是物理学家霍金的好友，他俩后来合作把彭罗斯的工作推广到宇宙学领域，证明了大爆炸一定始于一个奇点。

霍金与彭罗斯

彭罗斯的研究兴趣非常广泛，既有艰深的数学和物理，又有面向大众的趣味数学。他年轻时就跟他的父亲(一位精神病学家和遗传学家)一起设计了不可能在现实空间中实现的彭罗斯三角。

彭罗斯三角

彭罗斯三角可以利用视觉错觉来“实现”。比如下图中位于澳大利亚珀斯的这个雕塑，从特定方向看就是彭罗斯三角。

视觉错觉效果动图

奥地利的一个彭罗斯三角

这个比利时的彭罗斯三角采用了另外一种错觉设计：看起来像是直的，实际是弯的。

彭罗斯父子还创造了不可能实现的彭罗斯阶梯。

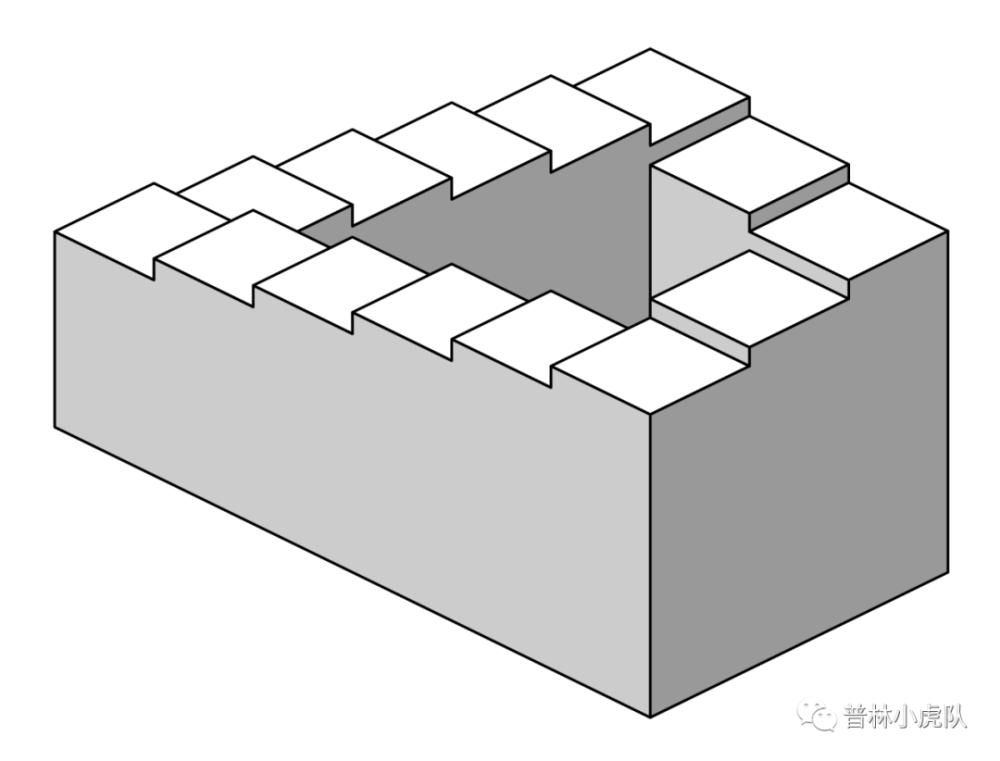彭罗斯阶梯

彭罗斯阶梯是荷兰版画大师埃舍尔作品《上升与下降》的主题。

在电影《盗梦空间》里友情出演

彭罗斯最著名的趣味数学发现当属彭罗斯镶嵌(Penrose tiling)。这里说的镶嵌就是用地板砖无缝铺满平面。我们最常见的地板砖是方形的，因为用同样大小的方形很容易铺满平面。我们也可以用同样形状和大小的三角形来铺满平面。

用香瓜的玩具拼出来的图

任意形状的三角形都可以铺满平面

任意形状的四边形都可以铺满平面

甚至这种奇形怪状的也能

有了三角形和四边形，下一个形状就是五边形。然而，同样形状和大小的五边形不能拿来铺满平面。无论怎么铺，总会有缝隙。

?下一个是正六边形，可以铺满平面。勤劳的小蜜蜂搭建的蜂巢就是这种形状。

前面几种铺满平面的方式都是周期性的，意思就是可以把所有地板砖朝某个方向平行移动一段距离，得到的铺法跟原来的还是分毫不差。比如方形的铺法，可以沿水平方向平移一个方格边长的距离，也可以沿竖直方向平移同样的距离，得到的铺法跟原来的一样。

彭罗斯在上世纪七十年代发现了彭罗斯镶嵌。这里的地板砖是两种不同形状但具有同样边长的菱形。一个菱形的四个角的角度分别是36°,144°,36°,144°，另外一个菱形的四个角度分别是72°,108°,72°,108°.

用这两种菱形可以造出无数个非周期性的铺法，比如下图。

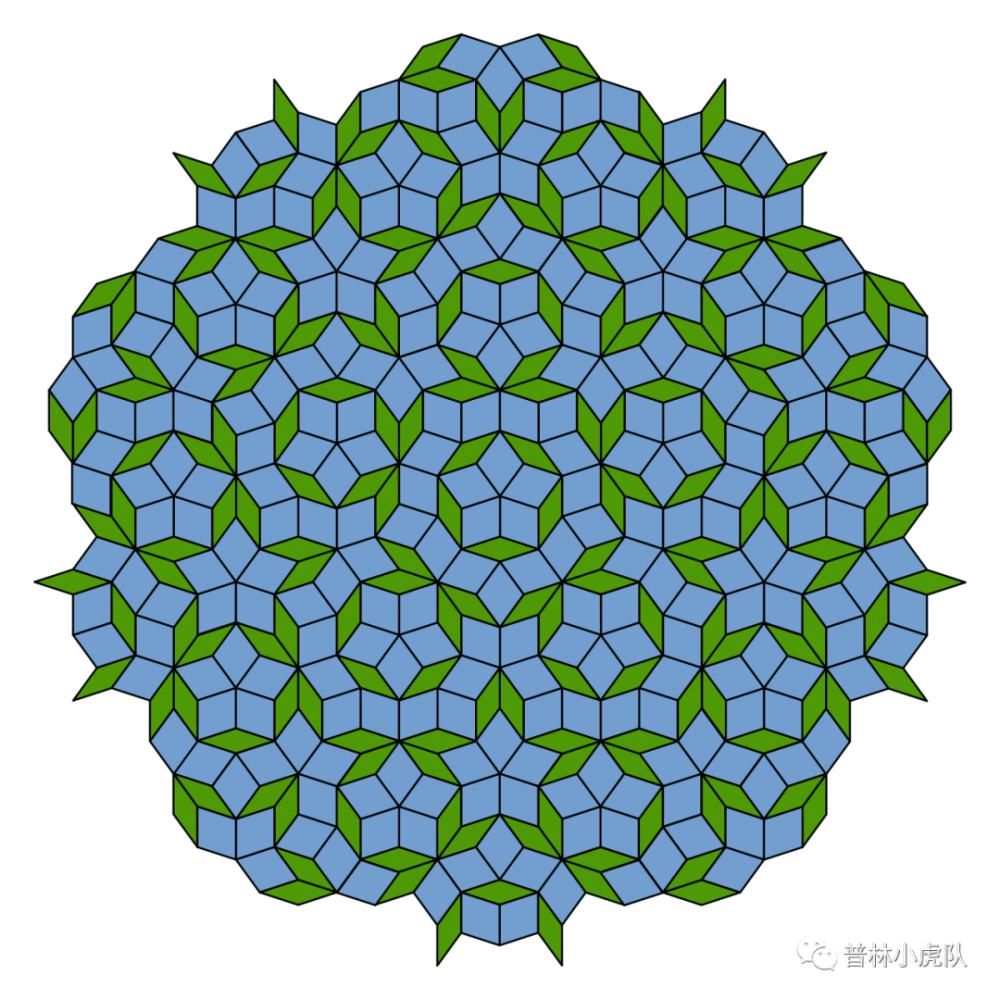令人惊异的是，尽管上图里的彭罗斯镶嵌不具有周期性，它仍然有五重对称性。也就是说，把这个图形绕某个中心点旋转72°（360°的五分之一），还是得到原来的图形。前面讲到的用三角形、四边形和正六边形铺满平面的方式都不具有五重对称性。

彭罗斯镶嵌的另外一种形式是使用以下两种“风筝”和“飞镖”形状的地板砖。

彭罗斯镶嵌的拼图积木

彭罗斯镶嵌还有许多奇妙的性质，跟一些深刻的数学理论有关。数学科普作家马丁·加德纳(Martin Gardner)曾写过多篇文章介绍彭罗斯镶嵌。

加德纳著作封面

彭罗斯镶嵌出现在很多设计中，像下面这张照片里彭罗斯爷爷脚下的地板。